指数関数のパラメータの推定
a1,をシフト
\(\Large \displaystyle y_i = a_0 \ Exp (- a_1 x_i) + a_2 \)
| a0 | 10.994 | 10.493 | 10.494 | 10.318 | 10.164 | 10.025 | 9.896 | 9.777 | 9.666 | |||
| a1 | 0.295 | 0.345 | 0.395 | 0.445 | 0.495 | 0.545 | 0.595 | 0.645 | 0.695 | |||
| δ | -0.2 | -0.15 | -0.1 | -0.05 | 0 | 0.05 | 0.1 | 0.15 | 0.2 | |||
| a2 | -0.679 | 0.000 | 0.279 | 0.612 | 0.884 | 1.109 | 1.297 | 1.457 | 1.592 | |||
| i | x | y | \( \hat{y} \) | |||||||||
| 1 | 0 | 10 | 10.315 | 10.493 | 10.774 | 10.930 | 11.048 | 11.133 | 11.193 | 11.233 | 11.258 | |
| 2 | 2 | 4 | 5.420 | 5.268 | 5.046 | 4.853 | 4.664 | 4.482 | 4.311 | 4.150 | 4.002 | |
| 3 | 3 | 2 | 3.864 | 3.732 | 3.492 | 3.331 | 3.189 | 3.066 | 2.960 | 2.870 | 2.795 | |
| 4 | 4 | 1 | 2.705 | 2.644 | 2.445 | 2.355 | 2.290 | 2.244 | 2.215 | 2.199 | 2.193 | |
| 5 | 6 | 0.5 | 1.199 | 1.328 | 1.263 | 1.329 | 1.407 | 1.491 | 1.577 | 1.661 | 1.742 | |
| 6 | 9 | 0.1 | 0.097 | 0.472 | 0.580 | 0.801 | 1.002 | 1.183 | 1.344 | 1.486 | 1.611 | |
| S (\(y_i - \hat{y} \)の平方和) | 2.988 | 1.704 | 0.819 | 0.381 | 0.2531 |
0.357 | 0.626 | 1.008 | 1.462 | |||
| dS (Seとの差分) | 2.734 | 1.451 | 0.566 | 0.128 | 0 | 0.104 | 0.373 | 0.755 | 1.208 | |||
・残差平方和
推定値からの残差
\(\Large \displaystyle Se = \sum_{i=1}^{n} \left[ y_i -\hat{a_0} \ Exp(- \hat{a_1} \ x_i) - \hat{a_2} \right]^2 \)
a0をシフトさせたときの,推定値からの残差
\(\Large \displaystyle Se = \sum_{i=1}^{n} \left[ y_i -\hat{a_0} \ Exp(- a_1 \ x_i) -\hat{a_2} \right]^2 \)
であり,a1を,δ,だけシフトさせて,固定し,その際のa0, a2の推定値をソルバーで推定しました.
dS,を見ていただけるとわかるように,推定値,Seが一番小さく,今回は,左右非対称に増加していることがわかります.
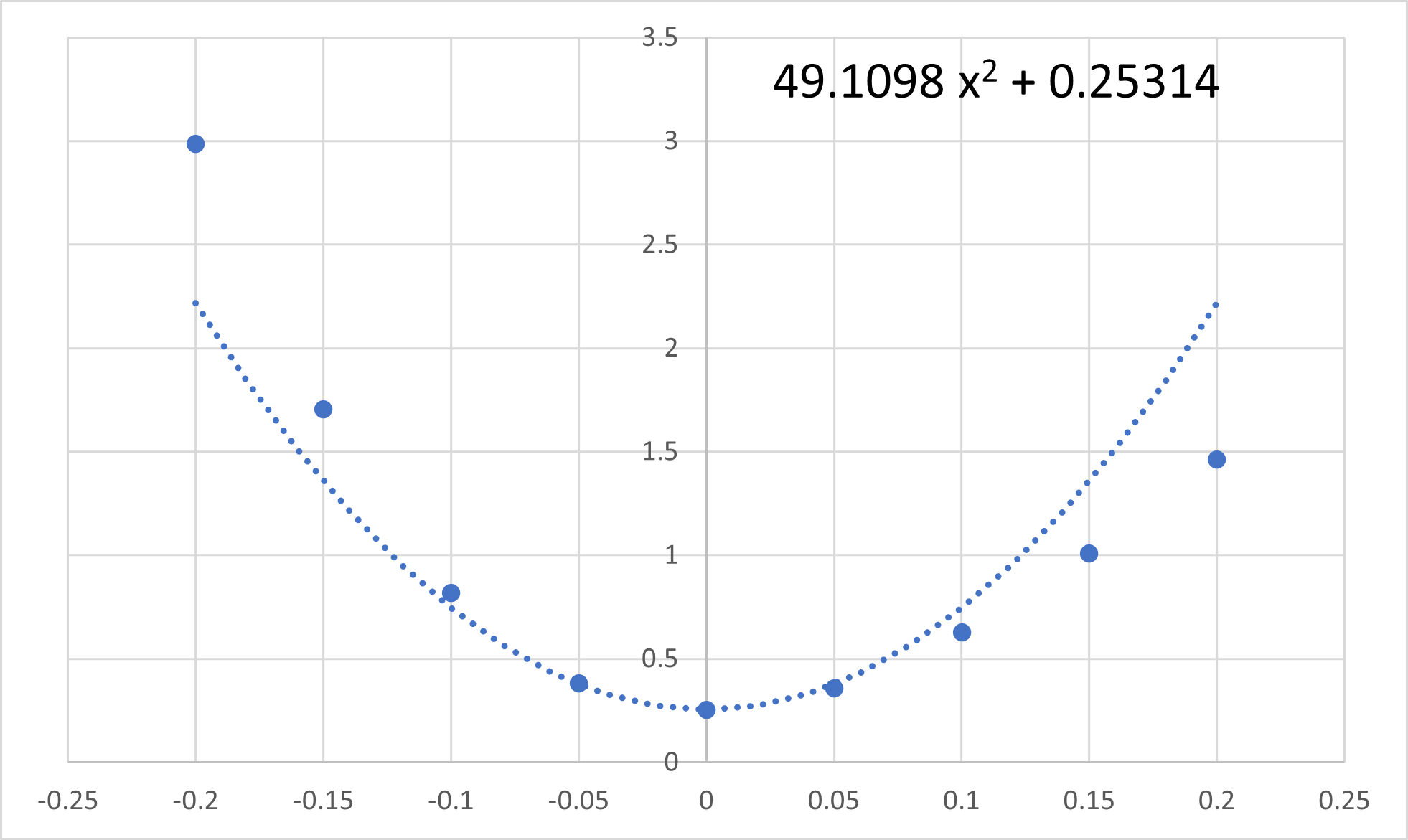
グラフ化すると,

のように,二乗+定数できれいに近似できます.
二次曲線の近似においてもきれいに近似でき,
\(\Large \displaystyle y = 0.2531 + 49.1098 \ \delta^2 \)
ここで,分散値は,
・分散
\(\Large \displaystyle Ve = \frac{1}{n-3} \sum_{i=1}^{n} \left[ y_i -\hat{a_0} \ Exp(- \hat{a_1} \ x_i) \right]^2 = \frac{Se}{n-3} = \frac{0.2531}{6-3} = 0.08438 \)
であり(a0,a1,a2の二つのパラメータが3つあるので,自由度は,n-3),
\(\Large \displaystyle 49.109 \ \delta^2 = 0.08438 \)
となるδがSEとなるので,
\(\Large \displaystyle \delta^2 = \frac{ 0.08438}{49.109} =0.00172 \)
\(\Large \displaystyle SE_{a_0} = \sqrt{\delta^2} =\color{red}{0.04145} \)
と推定できます.
・Rによる推定
Rでの近似を行ってみると,
プログラムは,
xx <- c(0,2,3,4,6,9)
yy <- c(11,5,3,2,1.5,1.1)
plot(xx,yy)
fm<-nls(yy~a0*exp(-a1*xx)+a2,start=c(a0=10,a1=0.5,a2=1),trace=TRUE)
summary(fm)
で,結果は,
| Parameters: | |||||
| Estimate | Std. Error | t value | Pr(>|t|) | ||
| a0 | 10.16402 | 0.37708 | 26.954 | 0.000112 | *** |
| a1 | 0.49456 | 0.04408 | 11.219 | 0.001518 | ** |
| a2 | 0.88393 | 0.26931 | 3.282 | 0.046348 | * |
となり,Kyplotにおいても,
| 推定値 | 標準誤差(SE) | |
| A1 | 10.16401 | 0.377081 |
| A2 | 0.494562 | 0.044083 |
| A3 | 0.883926 | 0.269308 |
と同じ結果となり,今回の推定値と,ほぼ一致,します.
微妙に異なるのが気になりますが....
「統計解析の初歩」,の「1.2 非線形最小2乗法の基本的な考え方」には,
δのずらした値0.5 を変えると結果は異なり、近似標準誤差の精度が変わる
統計パッケージにより、近似標準誤差の値は幾分異なる
とあります.ここで,”0.5”,がどこから出てきたかはわかりません.そもそも横軸(x軸)の範囲に依存しちゃいますし..
そこで,σをとる値(±での平均値)でどう推定値が変わるかを調べてみました.その結果が,
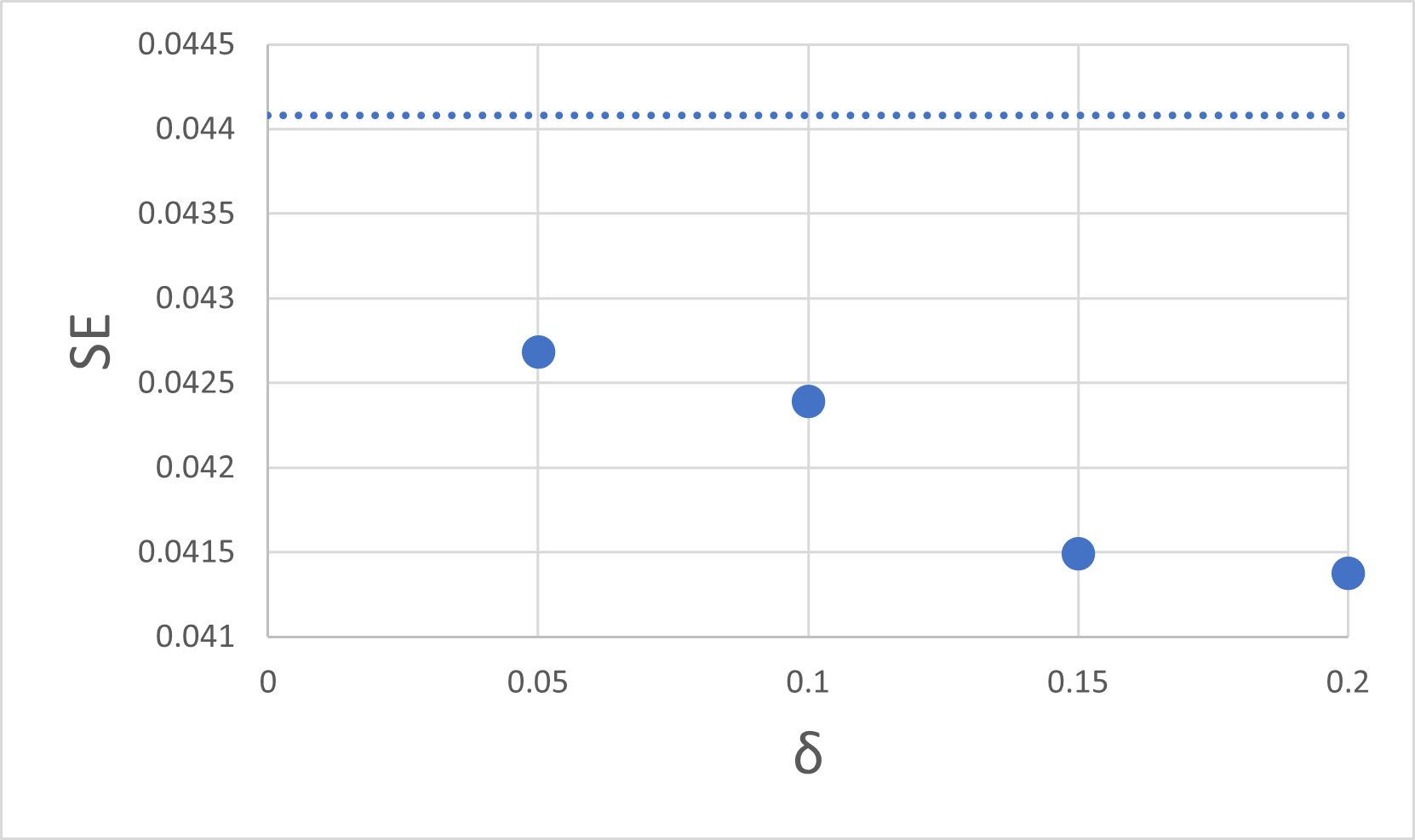
とどのδでもRなどの推定値より下回っていました....謎です...
次に,指数関数+baseのbaseのパラメータ,a2について,確認してましょう.